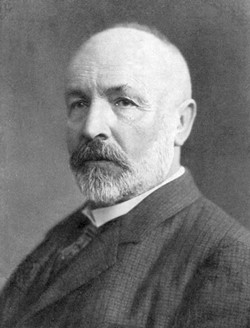Infinity and Beyond 

The concept of "infinity" has bothered and challenged philosophers for thousands of years, but the first really modern attempt at understanding it was made by the mathematician-astronomer-philosopher Galileo Galilei in his final book Two New Sciences (1638). The "Father of Modern Science" attributes our problems with infinity to the limitations of our brains, anticipating Emmanuel Kant's Critique of Pure Reason. Zeno's Paradox and all the other infinity-laden paradoxes arise when, in Galileo's words, "we attempt, with our finite minds, to discuss the infinite, assigning to it those properties which we give to the finite ..."

(Zeno of Elea, you may recall, had argued that in theory motion was impossible, since in order to traverse from A to B, you had to go halfway, which entailed going half of that distance, which entailed going half of that distance, ad infinitum. Since each step would take a finite length of time, you'd need an infinite amount of time to go anywhere.)

If it's true that the wise person solves the problem while the genius avoids it, the world must have been full of geniuses up until the 15th century. Aristotle, for instance, argued that infinity couldn't even be discussed because of the paradoxes that arise. Thomas Aquinas followed Aristotle's lead, as he usually did, saying that infinity is relegated to God (the original "uncaused Cause") and infinity is impossible in "real" time and space. So Galileo's forthright approach to the problem offered a fresh take on the subject.

Note that none of the pre-Galilean noodling had stopped mathematicians from actually using infinity. In proving that a sphere occupies exactly two-thirds of the cylinder into which it just fits, Archimedes conceptualized an infinite number of infinitely thin disks (anticipating calculus by over 2,000 years). Similarly, in 1609, Johannes Kepler derived his Second Law of Planetary Motion (planets sweep out equal areas with respect to the sun in equal times) by summing an infinite number of infinitely small triangles.

Turned out, Galileo and other mathematicians who followed him vastly underestimated infinity. Skipping many steps and missteps along the way, the Russian-German number theorist and philosopher Georg Cantor (1845-1918) wrestled the whole notion to the ground by showing that more than one type of infinity was possible. Before Cantor, we had finite "sets" (e.g. the set of your fingers) and infinite sets (the set of integers 1,2,3 ... to infinity). Cantor proved that the set of rational numbers (those that can be designated by a fraction, such as 191/7919) could be matched up one-to-one with the set of integers: every integer then has a corresponding rational number and vice versa. These two sets are thus equivalent and are "countably infinite" (or, denumerable).

He went on to show that "uncountably infinite" (nondenumerable) sets existed, such as the set of all possible ("real") numbers between 0 and 1, which include both rational and irrational numbers. Having proved the existence of at least one "type" of infinity, Cantor went on to show that many infinities — in fact, an infinity of infinities! — existed. In this way, Cantor founded the science of set theory, without which modern mathematics wouldn't exist.

Barry Evans ([email protected]) never got farther than Carl Sagan's "billions and billions" when it came to understanding really big numbers.